激活函數 Activation Function

接下上篇，我們繼續介紹較為常見的激活函數。

TanH/Hyperbolic Tangent 雙曲正切

TanH activation function 使用下列函數計算neuron的輸出:

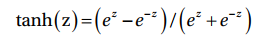
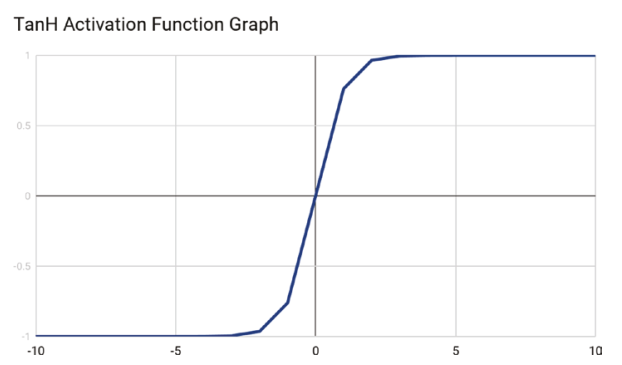
TanH與Sigmoid activation function 相當相似，除了TanH是以零值居中。圖中可明顯看出S型曲線有通過原點。
因為TanH函數是零值中心，它的模型輸入會有小，中與中間數值。

Rectified Linear Unit 線性整流函數

Rectified Linear Unit(ReLU) 根據z值來確定neuron的輸出。假設z值為正值，ReLU使用此數值當作neuron的輸出，反之輸出則為零。ReLU的輸出範圍位於0至+∞ 之間。
ReLU函數如下列所顯示:

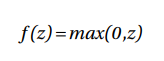
ReLu activation function的好處在於能夠有效計算及允許網路快速收斂。ReLu也是非線性且有導函數能夠套用於backpropagation，使得輸入權重能夠被修正。

ReLu activation function最大的缺點在於對於零或負值輸入，函數的梯度將會變成零值，這使得此方法不適合在輸入有負值的情況下使用。(無法套用backpropagation)
Z(X) = Relu(sum(Wi * Xi))，由此可知輸入(Xi)並和輸出(Z(X))並非線性關係，因此Relu並沒有限定輸入值域的問題。 (感謝Greysuki的指正~)

ReLU被廣泛使用於幾乎所有電腦視覺模組訓練上，像是圖片像素便不包含負值。

Leaky ReLU

Leaky ReLU提供ReLY的些微變化，取代了將z的負值變成零的方式，它將z的負值乘上極小數如0.01。
Leaky ReLU在負值區域有一段小斜坡且允許使用backpropagation。
但是缺點在於Leaky ReLU的負值結果並不保有一致性。

下篇接續!